The benefits of thermal mass may be illustrated by considering transient or changing heat flow conditions. When the temperature on one side of a wall in steady-state equilibrium is changed to another constant value, steady-state heat flow is not achieved immediately. Heat flow from the time the temperature is changed until steady-state conditions are reached is referred to as transient heat flow. The difference between steady-state and transient heat flow may be illustrated by considering idealized temperature profiles across a homogeneous wall section.
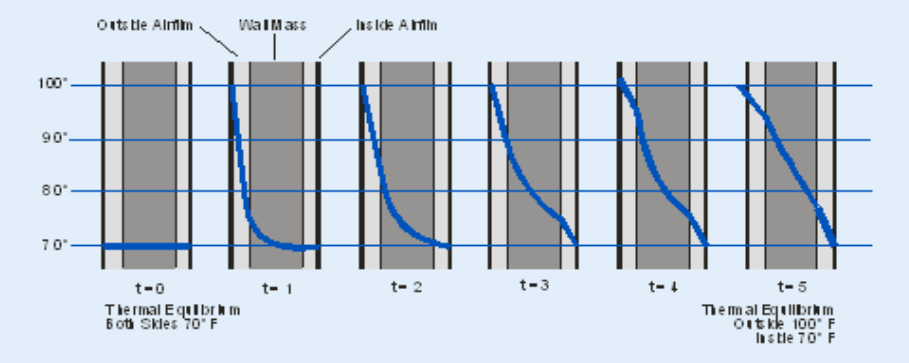
The figure shows the temperature profile (or gradient) through a mass wall at six-time intervals. The air films (surface conductance) are shown with exaggerated thickness for each time interval.
At t = 0, the outdoor surface of the wall and the outdoor surface temperatures are both 70 F and the homogeneous wall is in a steady-state condition. The temperature gradient is zero, and there is no heat flow through the wall. At t = 1, the outdoor temperature is increased to 100 F, which causes the outdoor surface temperature to increase. Heat enters the wall from the outdoors, but only that part of the wall close to the outdoor surface responds to the temperature change. No heat leaves or passes through the wall on the indoor side because the temperature gradient at the indoor surface is still zero.
The accumulated heat is being stored by the wall. At t = 2, t = 3, t = 4 and t = 5, more time elapses. At t = 1 and t = 2, heat enters the wall but does not pass through to the indoor surface. At t = 3 and t = 4, some heat is released to the indoor side of the wall. However, the heat entering the space is less than the amount entering the wall from the outdoors. For t = 1 through t = 4, heat is continually being stored by the wall. Heat flow predicted by U-value calculations will overestimate heat gains during periods illustrated by t = 1 through t = 4. Steady-state conditions are finally reached at t = 5. The temperature gradient is linear, and the amount of heat entering the wall is equal to the amount leaving.
Next: Material Properties